
목차)
1. 들어가기 전 이론
2. 라플라스 변환하기
1) 개념
2) 단위 임펄스 함수
3) 단위 계단 함수
4) 램프함수
5) 지수감쇠함수
6) 삼각함수
3. 응용하기
1) 시간 이동한 단위 계단함수
2) 거듭제곱 램프함수
3) 함수가 여러개인 경우
1. 들어가기 전 이론
1) 선형 방정식이란?
방정식 내에 제곱한 횟수인 차수의 최고값이 1을 넘지 않는 다항 방정식을 말함.
예시) 아래의 식들을 보면 모두 차수가 1을 넘지 않음.

2) 상미분 방정식이란?
한 개의 변수에 의존하는 미분방정식을 말함.
예시) 아래의 식들을 보면 출력의 y를 구하기 위한 변수가 1개 뿐인 것을 볼 수 있음.

제어 시스템 설계 시, 계산 식 중에서 선형 상미분 방정식을 계산할 때 라플라스 변환을 적용하면 간단히 해를 구할 수 있어 라플라스 변환은 반드시 알아 두어야 한다.
※ 상미분 방정식 외의 편미분 방정식(상미분과 다르게 변수가 두 개 이상인 미분 방정식) 계산은 라플라스 변환을 적용할 수 없고 수치해석을 따로 공부해서 해를 추측할 수 있다.
2. 라플라스 변환하기
1) 개념
선형 상미분 방정식 f(t)가 있는 경우, f(t)는 시간 공간에 있는 함수이다.
이것을 가상의 s공간에 가져와서 해당 성질에 따라 변형시키고 계산하는 개념이다.
그렇다면 변환 식은?

f(t)를 라플라스 변환한단 의미로 L[ f(t) ] 라 하고 결과 함수를 대문자로 s영역의 함수란 의미로 F(s)라 쓴다.
이것을 일일이 계산할 필요없이 보통 특정 함수에 따라 나타나는 결과식을 외우면 되는데 다음과 같다.
2) 단위 임펄스 함수

위의 사진을 보면 계단 한칸과 같은 그래프에 면적이 1인 파형을 볼 수 있다. 여기서 €에 0을 넣으면 해가 무한대가 되고 0이 아닌 값이 들어가면 0이 되는 함수를 단위 임펄스 함수이자 아래의 사친처럼 표현한다.

해당 함수를 라플라스 변환하면 결과는 1이 되는 것을 기억하면 된다.
3) 단위 계단 함수
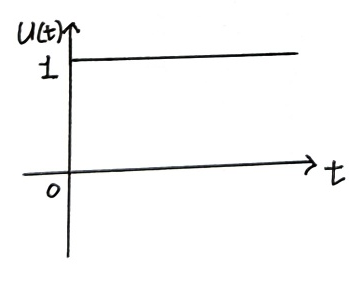
위의 사진과 같은 함수로 보통 u(t)라 쓴다. 이 함수를 라플라스 변환하면 다음과 같은 과정을 통해 1/s의 결과를 얻을 수 있다. 만약 앞에 상수 a가 있다면 상수는 그대로 통과되어 a/s라 쓰면 된다.
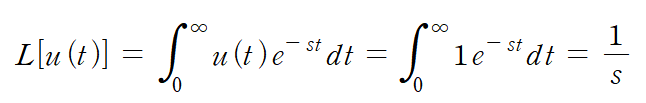
4) 램프함수
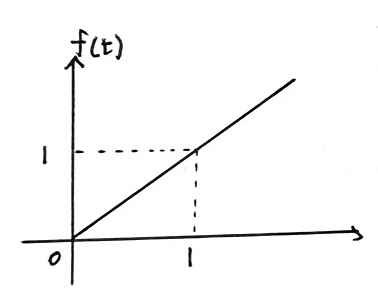
단위 계단 함수를 적분하여 얻을 수 있는 함수로 기울기가 1인 직선을 말한다. 라플라스 변환은 다음과 같은 과정을 통해 결과값을 얻을 수 있는데 역시나 상수a가 붙은 경우 상수는 그대로 통과되어 결과식에 곱해주면 된다.
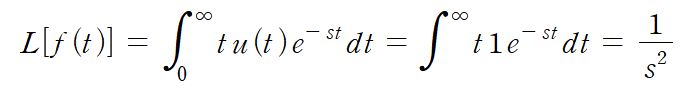
식을 구할 때 아래의 공식과 같은 부분적분 공식을 적용해야 풀 수 있다.
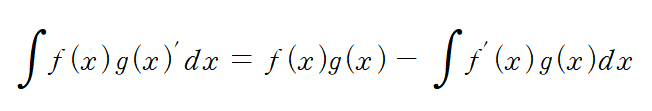
5) 지수감쇠함수
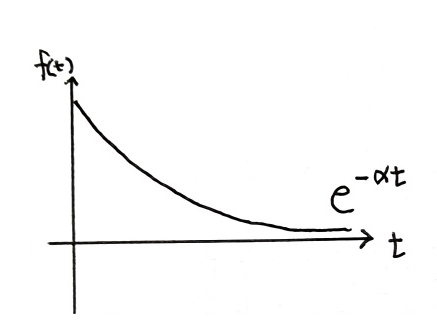
지수함수란 위의 사진처럼 시간의 양의 방향으로 증가하고 음의 방향에는 존재하지 않는 식을 말하며 반대로 지수감쇠함수는 시간의 양의 방향으로 감소하는 함수를 말한다. 해당 함수를 라플라스 변환하는 과정은 아래와 같다.
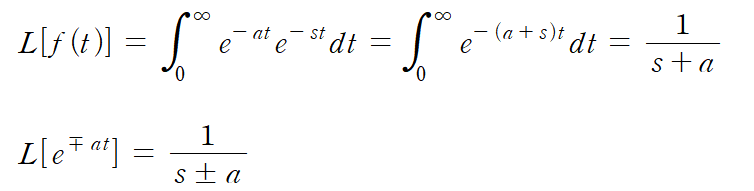
6) 삼각함수
삼각함수의 라플라스 변환도 라플라스 변화을 위한 식에 직접 대입하여 계산해서 익히는 것이 좋지만 삼각함수 쪽은 번거로우니 그냥 해당 결과식만 암기하기.
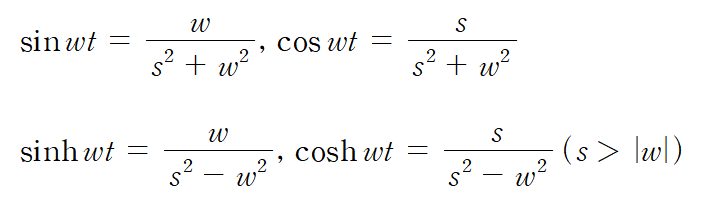
위의 1) ~ 6) 함수가 기본적으로 라플라스 변환을 공부하는 데 많이 사용하는 식인데 여기서 더 응용한 함수를 보자면 아래와 같다.
3. 응용하기
1) 시간 이동한 단위 계단함수
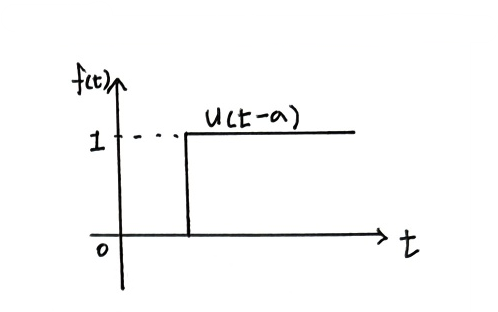
위의 사진처럼 그래프의 단위계단함수의 시간축이 a만큼 이동하였을 경우의 그래프로 라플라스 변환을 하면 아래의 과정과 같다.
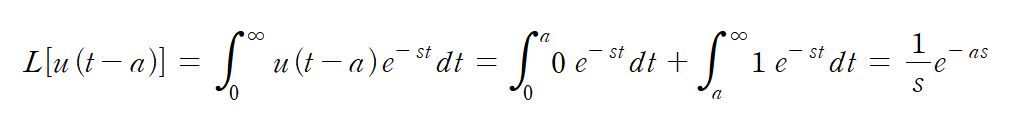
2) 거듭제곱 램프함수
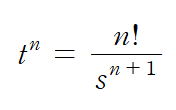
위에서 구했던 램프함수의 차수가 1이 아닌 2이상의 경우 결과식은 다음과 같으며 과정을 구해보는 것도 좋지만 조금 번거로울 수 있으니 옆의 결과식을 알아두는 게 낮다.
3) 함수가 여러개인 경우
위에서 구했던 1) ~ 6)의 기본 함수들이 만약 곱해져 있다면 라플라스 변환은? 위에서 구했던 결과식이 섞인 결과가 나온다. 따라서 직접 대입하는 것 대신에 위에서 알게 된 결과를 적용하는 방식으로 아래의 결과식을 익히면 된다.
예시는 아래와 같다.
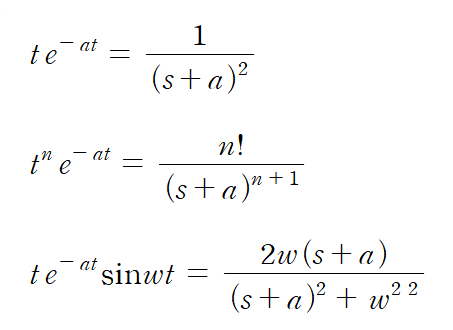
'공부 > 전기_자동제어' 카테고리의 다른 글
| 전기기사_자동제어_역라플라스 변환하기 (0) | 2024.09.02 |
|---|---|
| 전기기사 자동제어_라플라스 변환의 성질 (0) | 2024.08.31 |
| 자동제어 장치의 종류_조절부 동작에 따른 분류 (0) | 2024.08.23 |
| 자동제어의 정의 및 분류 (0) | 2023.06.26 |



