
목록
1. 들어가기 전 이론
2. 역으로 라플라스 변환하기
1) 이론
2) 근이 하나인 경우
3) 공액 복소근의 경우
4) 다중근의 경우
1. 들어가기 전 이론
라플라스 변환에 대해 잘 모른다면 반드시 아래의 링크들로 가서 먼저 이론과 특정 함수에서의 결과식 그리고 성질에 따른 변환에 대해 공부 후에 돌아오세요~
자동제어 기사 공부_라플라스 변환
목차)1. 들어가기 전 이론 2. 라플라스 변환하기1) 개념2) 단위 임펄스 함수3) 단위 계단 함수 4) 램프함수 5) 지수감쇠함수 6) 삼각함수3. 응용하기1) 시간 이동한 단위 계단함수 2) 거듭제곱 램
kongcong295.com
전기기사 자동제어_라플라스 변환의 성질
1. 들어가기 전 이론라플라스 변환이란?함수에 따른 라플라스 변환? 위의 질문처럼 성질을 알기 전에 알아야 할 이론이 궁금하시다면 ↓ ↓ ↓ 아래의 링크에 들어가주세요~라플라스 변환이란?
kongcong295.com
라플라스 변환을 통해 가상의 s영역의 함수로 바뀐 값을 다시 역으로 t의 시간 영역의 함수로 변환시키는 것이 역라플라스 변환이다.
2. 역으로 라플라스 변환하기
1) 이론
라플라스 변환의 결과식을 보면 아래와 같은 식의 형태를 많이 볼 수 있다.

해당 식은 바로 지수함수의 라플라스 변환값임을 금방 알 수 있다. 이외에도 특정 함수에 따라 해당 라플라스 변환 형태가 나온다는 점을 이용해서 역라플라스 변환을 계산하는데 그 중에서 위의 결과식을 역변환하기 편하므로 라플라스 변환값을 부분 분수로 전개해서 푸는 방식을 많이 쓴다.
※ 라플라스 변환 문제를 많이 풀었다면 특정 값을 보면 변환 이전의 시간t 공간에서의 원래 식을 유추 할 수 있다. 만약 보이지 않는다면 아직 라플라스 변환에 많이 익숙하지 못한 것이니 좀 더 문제를 직접 많이 풀어 볼 것.
그럼 예시를 들어 역라플라스 변환하기 설명하면 아래와 같다.
2) 근이 하나인 경우
근이 하나인 아래의 식 같은 경우 다음과 같이 역변환 하기 쉽도록 바꿀 수 있다.

여기서 K의 값을 구해야하는데 먼저 첫번째 식의 양 쪽 식에 (s-p1)을 분자에 곱한 상태에서 s=p1을 넣으면 오른쪽 식에선 K1하나만 남고 왼쪽 식에선 값이 나오게 된다. 이런식으로 차례로 (s-p2), (s-p3) ~ (s-pn)까지 분모에 곱해서 해당 K값을 구하면 아래의 식처럼 역변환하기 좋은 식이 만들어진다.

3) 공액 복소근의 경우
위의 근이 하나인 단근처럼 풀기 편한 부분 분수 형태로 바꾸는 점은 같지만 위와 다르게 공액 복소근이 포함된 경우 계산이 늘어난다.

식만 보았을 땐 이해하기 어렵다. 일단 첫 번째 식에서 K값을 구하기 위해선 위의 단근을 구했을 때와 같이 계산하면 된다. 대신 C와 D를 구하기 위해선 두 식에 모두 분자에 (s-a)제곱 + w의 제곱을 대입한 뒤에 s에 a+jw를 넣어서 구한다. 그럼 나머지 변수도 구해지는데 식을 역변환하게 되면 아래의 식과 같다.
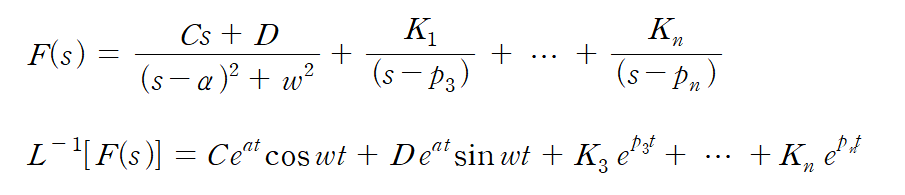
4) 다중근의 경우
앞의 경우들은 그나마 계산하기 크게 어렵지 않지만 변수의 차수의 최댓값이 2이상인 다중근의 경우는 계산이 더 추가되서 번거롭지만 크게 어렵진 않으니 아래의 식을 보고 따라하면 된다.
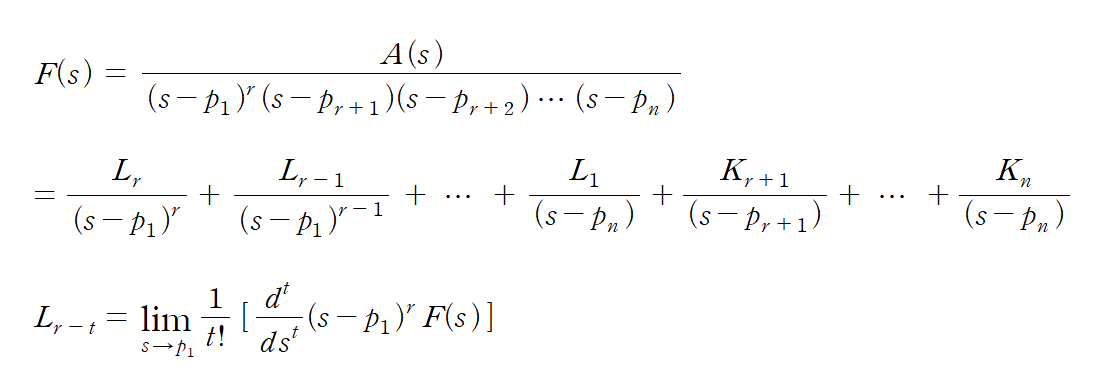
이렇게 보면 역시나 어려운데 먼저 맨 위의 식에서 다중근 외의 근은 앞의 단근을 구할 때처럼 K를 구하면 된다. 그런데 다중근은 아무래도 변수의 차수만큼의 근이 생기기 때문에 L값들이 생겨난다. 그럼 L을 구하기 위해선 가장 아래의 식처럼 일일이 다중근의 최대 차수가 되는 만금의 s-p를 곱해주고 미분도 해주어야 한다. 역시 이렇게 말해도 이해하기 어려울테니 아래의 예시 문제를 풀이하면서 익힐 것.
예시) 85년 산업기사 출제문제

가장 먼저 식을 부분 분수 형태로 풀어쓴다.
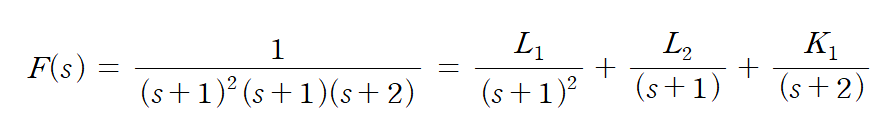
여기서 L을 구하기 위해선 아래와 같이 위에서 언급한 식대로 풀어준다.
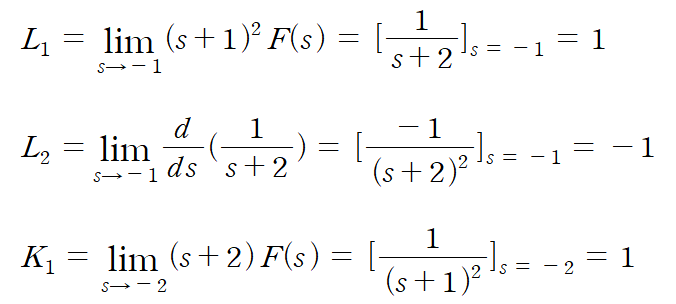
따라서 변수를 대입한 식을 역변환하게 되면 아래의 값을 구할 수 있다.
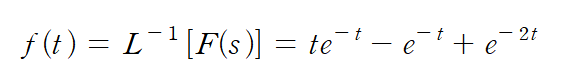
다중근 문제가 나오면 위의 방법처럼 차례대로 계산하면 어렵기 보단 귀찮아질테니 꼭 문제를 자주 풀어보면서 익혀볼 것.
'공부 > 전기_자동제어' 카테고리의 다른 글
| 전기기사 자동제어_라플라스 변환의 성질 (0) | 2024.08.31 |
|---|---|
| 자동제어 기사 공부_라플라스 변환 (0) | 2024.08.30 |
| 자동제어 장치의 종류_조절부 동작에 따른 분류 (0) | 2024.08.23 |
| 자동제어의 정의 및 분류 (0) | 2023.06.26 |



